• お役立ちコラム

【算数】小学5年生がつまずきやすいポイントは？解消するためには

小学5年生の算数は、これまで学んだ基礎を活用し、さらに発展的な内容に取り組む学年です。
そして難易度の上昇や内容の複雑化により、多くの生徒が「つまずき」を感じやすい時期です。

今回は小学5年生でつまずきやすい算数のポイントと対策をご紹介します！

速ドッグロボ

小学5年生の算数でつまずきやすいポイント

つまずきやすいポイントはいくつかありますが、難易度の上昇により、授業の速度についていけなくなることもあります。
学校の授業の復習や、宿題にどれくらいじっくり取り組んでいるかという家庭学習の状況によっても差が生まれやすくなります。

計算の難易度が上がる

小学5年生の算数では、これまでよりも計算の難易度が上がります。
例えば、小数や分数のかけ算・わり算を学ぶようになり、計算方法を正確に理解して手順通りに進める力が求められます。
これらは低学年で習った四則計算（たし算、ひき算、かけ算、わり算）がしっかり身についていないとつまずきやすい部分です。

分数と小数が理解できていない

小学5年生の算数でつまずきが多い分野のひとつが、分数と小数の計算です。
分数のたし算やひき算では「通分」という新しい手順が追加され、小数では位取りを意識しながら計算を行わなければならないため、難しいと感じる子どもが増えます。
小数の「ひっ算」で、位がズレてしまって計算問題での不正解が増えてしまい、苦手になっていくケースもあります。

特に、分数や小数の概念自体があいまいな場合、計算に対する苦手意識が強まってしまいます。
このような苦手意識は、算数全体に対する苦手意識につながりやすいので、早めに理解を深めることが必要になります。

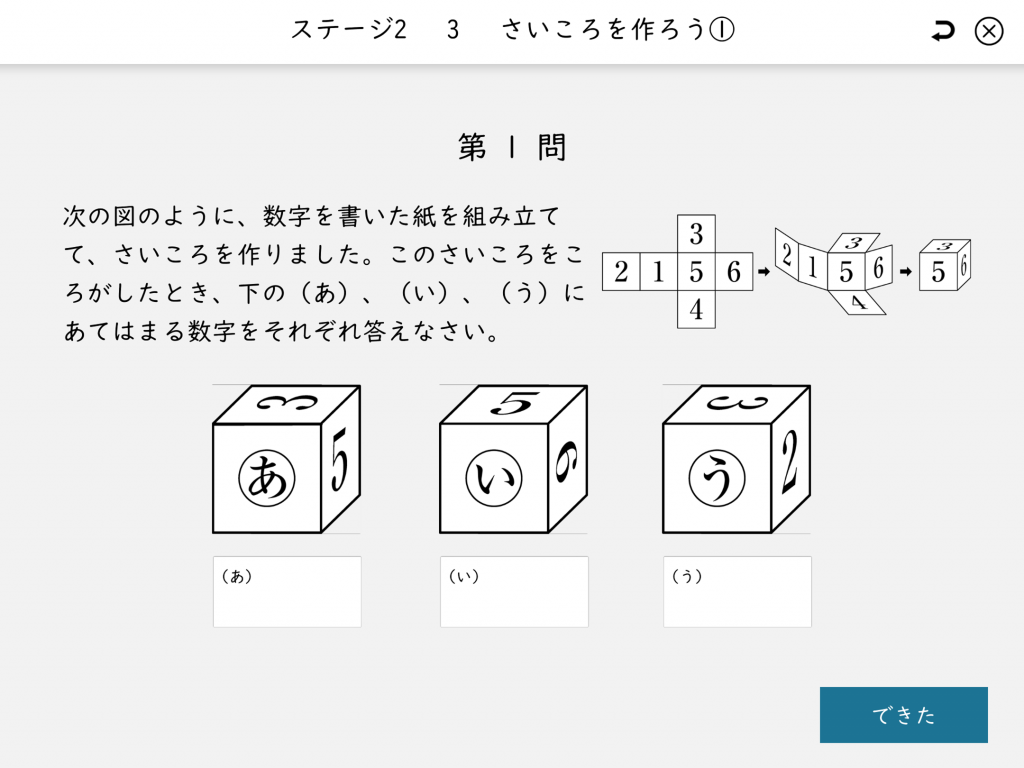
図形問題をイメージして解けない

小学5年生では直方体や立方体の体積、三角形や台形などの面積を求める計算が中心となります。
しかし、図形を頭の中でイメージする力に個人差が出るため、この段階でつまずくこともあります。
特に、平面から立体を想像することが難しい場合や、公式を丸暗記しているだけで実際の図形の性質を理解できていない場合（例えば、三角形の面積を求める公式は「底辺×高さ÷2」ですが、どこが高さかわからないなど）に「つまずき」が発生してしまいます。

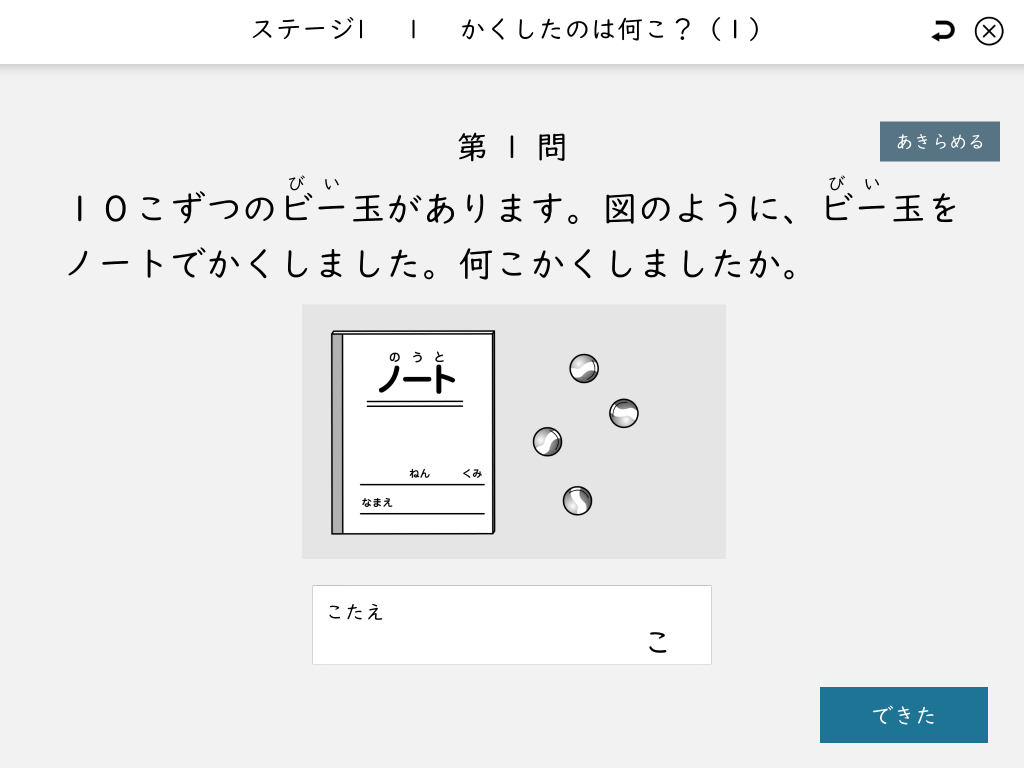
複雑な文章題に対する苦手意識

文章題は理解力や読解力だけでなく、論理的に思考する力を必要とするため、苦手意識を持ちやすい分野です。
特に「割合」や「速さ」の単元では、問題文の中の数字や条件を正確に読み取ることが求められます。
これが難しいと、そもそも何を求めればいいのか分からなくなり、解答にたどり着けない状態になりがちです。

さらに、複数の計算工程が必要になる問題も増えるため、「どこから始めれば良いのかわからない」と混乱する場合があります。

小5の算数、つまずきを早めに解消するには

算数は「積み上げの科目」と言われるほど、基礎的な学習内容がその後の理解に大きな影響を与えます。

速ドッグロボ

特に小学5年生になると、計算の難易度が上がるだけでなく、「割合」や「比例」といった新しい概念も登場し、つまずきやすくなるのが特徴です。
これらを早めに解消することで、算数の学習をスムーズに進めることができます

分数を正確に理解する（通分や計算の手順）

小学5年生の算数では、分数の計算が重要なテーマとなります。

しかし、分数を正確に理解できていないと、計算が混乱し、他の単元にも悪影響を及ぼします。
特に「通分」の手順を理解することが重要です。
また、この段階で計算ミスをしやすい子どもも多いので、繰り返し練習を重ねると良いでしょう。

さらに、分数のかけ算やわり算も学習しますが、ここでは数の大小関係が重要になります。 例えば、「1/2 × 3/4」や「3 ÷ 1/5」のような問題では、数の意味をイメージしながら解くことが求められます。
こうした分数計算が理解できていないと、後に学ぶ「割合」や「速さ」といった単元でもつまずきやすくなります。

小学校卒業後も必要な「計算の基礎」をマスターする

小学校5年生で学んだ計算の基礎は、中学校以降の数学にもつながる非常に重要な内容です。

例えば、小数のかけ算やわり算、分数の計算は中学での方程式や関数で繰り返し使用されます。
特に「比例」や「割合」の単元は、速さや割合のグラフに関連し、日常生活でも活用される場面が多いため、しっかりとマスターしておきたい分野です。

算数におけるつまずきは、小学校高学年で顕著になりやすいですが、その原因が低学年の基礎部分であることも少なくありません。
したがって、どこでつまずきが発生しているのかを正確に把握し、それを復習しましょう。
計算の基礎をしっかり固めることで、小学校卒業後もその学習が役立つ大きな一歩となります。

つまずきを解消する方法

では、具体的にはどうすればいいのでしょう？

つまずきを放置せず、基礎の見直しと学習方法の工夫によって、確実に理解を深めていくことが大切です。

今日から実践していきましょう！

速ドッグロボ

反復学習で基礎を固める

算数は積み上げの教科であるため、小学5年生でのつまずきはこれまで学んできた基礎知識の定着不足が原因になりがちです。
そのため、反復学習が非常に重要になります。
特に「分数の計算」や「わり算」など、算数の基本となる内容を何度も練習し、手順を身に付けることで自信を取り戻すことができます。

例えば、類題を繰り返し解いて手順を定着させたり、少し易しい問題や過去の学年の教材を使って基礎から復習させたりすると良いでしょう。
また、ミスをする箇所を分析し、その部分を集中して対策することも有効です。

生活の事例でイメージをする

算数がわからなくなる要因の一つは、学んでいる内容が身近な生活に結び付けられていないことです。

例えば、「割合」や「比例」の学習では、買い物の値引きや料理のレシピなど身近な事例を活用すると良いでしょう。
「スーパーで20%オフの値段を計算するには？」、「このレシピは2人用だけど、家族4人分にするには？」といった具体的な場面に当てはめて考えると、学習内容をより理解しやすくなります。
算数を日常生活と結び付けることで、抽象的な内容も実感を持って学べるようになるでしょう。

文章問題のために読解力を育む

複雑な文章問題へのつまずきを防ぐためには、算数だけでなく読解力を高めることが重要です。

文章問題を解くには、書かれている条件や問いを読み取り、数式や考え方に落とし込む力が求められます。
低学年のうちは、問題文中の数字を出ている順に計算すれば正解が出る問題が多かったのに対し、高学年になると必要な情報を見つけ出して正しく立式する問題が増えてきます。
そのため、日常的に文章を読む習慣をつけることが効果的です。

また、文章問題を解く際は、まず条件を整理し、図や表を使って視覚的に情報を整理することも有効です。
問題文の中のキーワードや数字に注目させる練習を繰り返すことで、文章の意味を正確に理解できる力が身につきます。

計算を繰り返しトレーニングする

小学5年生の算数では、難易度の高い計算問題が増えるため、計算力が十分に身についていないとつまずきやすくなります。そのため、日々の繰り返しトレーニングが必要です。

例えば、毎日短時間で計算問題に取り組む習慣を設けるのも良いでしょう。
最初は簡単な問題から始め、徐々に難易度を上げていく方法がおすすめです。

また、間違えた問題を復習して「なぜ間違えたのか」を考えることで、苦手分野の克服に繋がります。
こうした積み重ねが、算数全体のつまずきの解消へとつながります。

総合的な思考力を身につけ、算数・数学が得意に！算数的思考力講座

算数的思考力講座では、基礎となる計算力をトレーニングし、すばやく正確に処理できる力を身につけていきます。
その上で、思考問題の基本パターンを習得しながら、どのような問題に直面しても、深く考え抜いて解決する力を養成していきます。

整数の計算から単位換算や割合計算など、約40のカテゴリの計算問題でパターンを習得し、反復により速度をの向上を目指します。

算数的思考力トレーニングは、好学出版『算数ラボ』、『算数ラボ２』、『算数ラボ図形』から 1000 問以上抜粋して搭載。
NeU監修の思考力トレーニングは、知能の基礎となる認知能力のパフォーマンスを高めます。

監修

安田哲

一般社団法人 日本速読解力協会 理事

約20年間にわたり首都圏大手進学塾の現場の最前線で、英語・国語を中心に指導。中学受験・高校受験の難関校への多数の合格者を輩出。科目の内容の指導だけでなく、家庭学習管理、生徒・保護者の皆様との面談を多数行う。大学院では言語学を専攻、英語以外の言語に関しても幅広い知識を有する。

詳細はこちら